RATIO PROPERTIES: AZIMUTH
Azimuth is the factor distinguishing the size of a timespan in comparison to an adjacent timespan. The functional range of the azimuth extends from symmetry, where two adjacent timespans are of equal length (1:1), to simultaneity, where one timespan is eclipsed by the other, and their effective ratio is an irrational "0:1".
The term is not a familiar one to music theory because most of our conversations about rhythm and note values are concerned with division and multiplication -- the quantity of smaller parts into which a unit is divided or subdivided, or the factor by which a small part is multiplied to produce a measure or hypermeasure. When we think of ratios in metric hierarchies we are normally thinking of each number in the ratio as representing a different way of dividing a single timespan. This enables us to imagine more than one tempo simultaneously; each tempo is made of a succession of overlapping 1:1 ratios, with each succession occurring at a different speed. By contrast, the ratios described here will be juxtapositions of successive timespans--I will call these "timespan ratios". Each ratio will assume (for now) the persistence of at least one very small, and adjacently repeating, duration, that serves as an unchanging unit for the measurement of larger values.
This requires temporary sacrifices: we lose the ability to conceive of values that aren't multiples of the unchanging unit, and we lose the enticing notion of multiple, simultaneous tempos. But in exchange for the sacrifice, we gain some facility with our thinking about different qualities of relationship that one timespan followed by another can produce. Although we are restricted to whole numbers in dealing with the unit, we have no restrictions in describing timespan relationships: the ratio "1.5 : 4" is expressed "3 : 8"; the ratio "3.0399 : 12" is expressed "10133 : 40000" (multiply by whatever you need to get to the most "reduced" whole number form of the ratio -- in this case, the factor was a third of 10,000). The latter ratio is a little silly, since at virtually any musical tempo it will be hard to distinguish it from the familiar "1:4." But not all large ratios "round off" as easily -- 8:21 can sound like 2:5 in some contexts and 1:3 in others, but it might also be a distinctive percept, worth exploring in its own right.
Initially the discussion will be restricted to groups of two adjacent timespans. One way to imagine the gamut of relationships available for timespan ratios is to think of a two-dimensional grid as though it were a simple fascimile of the ancient Parthenon. In the grid, 1st-member values for a ratio will appear along one side, and 2nd-member values along another. Figure 1 might be a Parthenon-like monument with 49 columns:
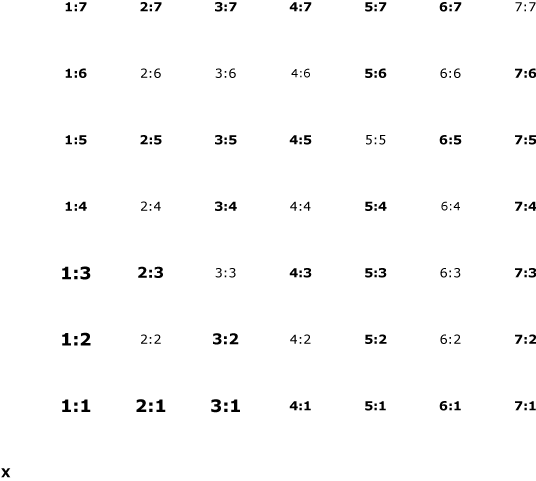
Here we obviously have all the ratios containing timespans of length 1 through 7, arranged in a logical, rather than intuitive way. But if we imagine ourselves as perceivers of timespan ratios, there might be some intuitive value to locating ourselves at the spot marked "x" in the lower left-hand corner, gazing diagonally up and to the right across the grid. (Our field of vision, in that case, might be structured a little like this popular Athenian postcard view.)